
【导读】【每日一练】高阶导数的应用。重庆教师招聘考试复习资料2021.1.5。更多教师招考信息,备考干货,辅导课程,时政资料,欢迎关注重庆教师招聘网。
高阶导数的应用
应用一:判断函数凹凸性
1.函数的凹凸性定义:
设![]() 在区间I上连续,如果对I上任意两点
在区间I上连续,如果对I上任意两点![]() ,
,![]() 恒有
恒有 ,则称
,则称![]() 在I上的图形是(向上)凹的;如果恒有
在I上的图形是(向上)凹的;如果恒有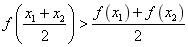 ,那么称
,那么称![]() 在I上的图形是(向上)凸的。
在I上的图形是(向上)凸的。
2.判断函数凹凸性:
设函数![]() 在
在![]() 上连续,在
上连续,在![]() 内具有一阶和二阶导数,那么
内具有一阶和二阶导数,那么
(1)若在![]() 内
内 ,则
,则![]() 在
在![]() 上的图形是凹的;
上的图形是凹的;
(2)若在![]() 内
内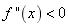 ,则
,则![]() 在
在![]() 上的图形是凸的。
上的图形是凸的。
应用二:判断函数拐点
1.函数拐点的定义:
一般地,设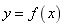 在区间I上连续,
在区间I上连续,![]() 是I内的点,如果曲线
是I内的点,如果曲线 在经过点
在经过点 时,曲线的凹凸性改变了,那么就称点
时,曲线的凹凸性改变了,那么就称点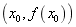 为这曲线的拐点。
为这曲线的拐点。
2.判定区间I上的连续曲线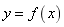 的拐点:
的拐点:
(1)求![]() ;
;
(2)令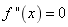 解出这方程在区间I内的实根,并求出在区间I内
解出这方程在区间I内的实根,并求出在区间I内![]() 不存在的点;
不存在的点;
(3)对于(2)中求出的每一个实根或二阶导数不存在的点![]() ,检查
,检查![]() 在
在![]() 左、右两侧临近的符号,那么当两侧的符号相反时,点
左、右两侧临近的符号,那么当两侧的符号相反时,点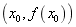 是拐点,当两侧的符号相同时,点
是拐点,当两侧的符号相同时,点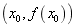 不是拐点。
不是拐点。
【2018重庆试题】(多选题)
关于曲线 ,下列说法正确的是( )。
,下列说法正确的是( )。
A.![]() 为凹区间 B.
为凹区间 B.![]() 为凸区间
为凸区间
C.![]() 为拐点 D.
为拐点 D.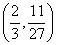 为拐点
为拐点
【答案】ABCD
【解析】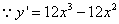 ,
, ,
,
令![]() ,解得
,解得![]() 或
或![]() ,
,
所以当![]() ,即
,即![]() 或
或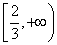 是该函数的凹区间,
是该函数的凹区间,
当![]() ,即
,即![]() 是该函数的凸区间;
是该函数的凸区间;
而点![]() ,
,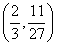 都在曲线
都在曲线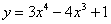 上,
上,
且两点的二阶导数在左右两侧异号,
故![]() 和
和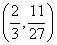 是函数的拐点。
是函数的拐点。
故本题答案为ABCD。
【课程推荐】
教师面试《数学》说课+试讲
 地区
地区 考试科目
考试科目 微信
微信

 微博
微博 抖音
抖音 023-67417095
023-67417095


















 点击关注
点击关注











