
【导读】【每日一练】函数的概念和性质。重庆教师招聘考试复习资料2021.11.16。更多教师招考信息,备考干货,辅导课程,时政资料,欢迎关注重庆教师招聘网。
一、必备基础知识
1、常见函数定义域:
(1)分母不能为零 (2)偶次根号下的数大于等于零
(3)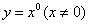 (4)
(4)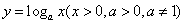
(5)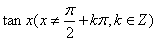
2、抽象函数定义域
求复合函数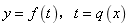 的定义域的方法:
的定义域的方法:
①若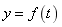 的定义域为
的定义域为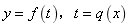 ,则解不等式得
,则解不等式得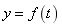 即可求出
即可求出![]() 的定义域;
的定义域;
②若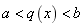 的定义域为
的定义域为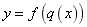 ,则求出
,则求出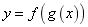 的值域即为
的值域即为![]() 的定义域。
的定义域。
3、求函数的值域常见方法:
(1)直接观察法:![]() ,
,![]() ,
,![]() ,
,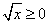 ,
,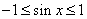 等等。
等等。
(2)配方法:主要针对二次函数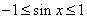
(3)换元法:将函数中的其中一个量看成一个整体设为![]() ,然后要注意
,然后要注意![]() 的取值范围。
的取值范围。
(4)分离常数法:形如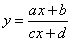 等,
等,
(5)数形结合法:主要针对含有绝对值的函数,需要取绝对值讨论。
(6)判别式法:主要针对分子分母含有二次函数类型。
4、函数的单调性
|
|
增函数 |
减函数 |
|
定义 |
一般地,设函数 |
|
|
当 |
当 |
|
|
图象 描述 |
自左向右图像是上升的 |
自左向右图像是下降的 |
判断函数单调性的常用方法:
(1)定义法(熟练利用定义法证明函数单调性的步骤).
(2)两个增(减)函数的和仍为增(减)函数;
一个增(减)函数与一个减(增)函数的差是增(减)函数.
(3)奇函数的单调性相同,偶函数的单调性相反。
(4)导数法:求导判断
(5)复合函数:记住“同增异减”
熟记以下几个结论:
(1)![]() 与
与![]() 的单调性相同;
的单调性相同;
(2)![]() 与
与![]() 的单调性相反;
的单调性相反;
(3)![]() 与
与![]() 的单调性相反。
的单调性相反。
4、函数的奇偶性
一般地,如果对于函数![]() 的定义域内任意一个x,都有
的定义域内任意一个x,都有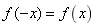 ,那么函数
,那么函数![]() 就叫做偶函数.
就叫做偶函数.
一般地,如果对于函数![]() 的定义域内任意一个x,都有
的定义域内任意一个x,都有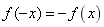 ,那么函数
,那么函数![]() 就叫做奇函数.
就叫做奇函数.
奇函数的图像关于原点对称;偶函数的图像关于![]() 轴对称.
轴对称.
常见偶函数有:![]() ,
,![]() ,
,![]() ,
,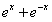 等等。
等等。
常见奇函数有:x,![]() ,
,![]() ,
,![]() ,
,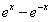 ,
,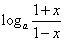 ,
,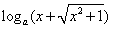 等等。
等等。
定义的应用:若函数y=f(x)是偶函数,则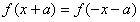 ;若函数
;若函数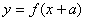 是偶函数,则f(x +a)= f(一x +a).
是偶函数,则f(x +a)= f(一x +a).
.
奇偶函数的常见性质:
(1)如果奇函数f(x)在x=0处有定义,则f(0)=0;
(2)如果函数f(x)的定义域不关于原点对称,那么f(x)一定是非奇非偶函数;
(3)如果f(x)既是奇函数又是偶函数,那么f(x)的表达式是f(x)=0.
(4)奇函数在关于原点对称的区间上的单调性相同,偶函数在关于原点对称的区间上的单调性相反.
(5)在公共定义域内
①两个奇函数的和是奇函数,两个奇函数的积是偶函数;
②两个偶函数的和、积都是偶函数;
③一个奇函数,一个偶函数的积是奇函数.
判断函数奇偶性的步骤:
(1)首先确定定义域,并判断其定义域是否关于原点对称;
(2)确定f(x)与f(-x)的关系;
(3)下结论。
5、函数的周期性
(1)周期函数:对于函数y=f(x),如果存在一个非零常数T,使得当x取定义域内的任何值时,都有f(x +T)= f (x)
,那么就称函数y=f(x)为周期函数,称T为这个函数的周期。
(2)最小正周期:如果在周期函数f(x)的所有周期中存在一个最小的正数,那么这个最小正数就叫做f(x)的最小正周期.
常见函数周期求法:
(1)若对于R上的任意的![]() 都有f(2a-x)= f (x)
都有f(2a-x)= f (x)
或f(一x)= f(2a+x)
,则x=a的图象关于直线R对称.
(2)若对于R上的任意x都有f(2a-x)= f (x),且f(2b-x)= f(x)
(其中a<b),则:y=f(x) 是以2(b-a)为周期的周期函数。
(3)若f(x+a)或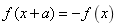 或
或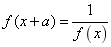 ,那么函数
,那么函数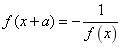 是周期函数,其中一个周期为
是周期函数,其中一个周期为![]() ;
;
(4)若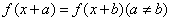 ,那么函数f(x)是周期函数,其中一个周期为
,那么函数f(x)是周期函数,其中一个周期为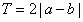 .
.
6、函数图象变换:
(1)平移变换:熟记口决:左加右减,上加下减。
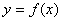 的图像向左平移
的图像向左平移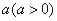 个单位得到函数
个单位得到函数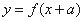 的图像;
的图像;
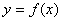 的图像向右平移
的图像向右平移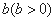 个单位得到函数
个单位得到函数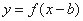 的图像;
的图像;
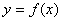 的图像向上(下)平移
的图像向上(下)平移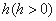 个单位得到函数
个单位得到函数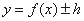 的图像。
的图像。
(2)对称变换:
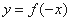 与
与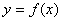 的图像关于
的图像关于![]() 轴对称;
轴对称;
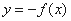 与
与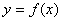 的图像关于
的图像关于![]() 轴对称;
轴对称;
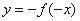 与
与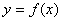 的图像关于原点对称。
的图像关于原点对称。
(3)翻折变换:
①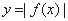 的图像:先画出
的图像:先画出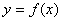 的图像,然后保留x轴上方部分,并把
的图像,然后保留x轴上方部分,并把![]() x 轴下方部分翻折到x轴的上方即可。
x 轴下方部分翻折到x轴的上方即可。
② 的图像:先画出
的图像:先画出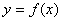 的图像,然后保留y轴右侧部分,并把 y 轴右侧部分翻折到y轴的左侧即可。
的图像,然后保留y轴右侧部分,并把 y 轴右侧部分翻折到y轴的左侧即可。
教师面试《数学》说课+试讲
 地区
地区 考试科目
考试科目 微信
微信

 微博
微博 抖音
抖音 023-67417095
023-67417095


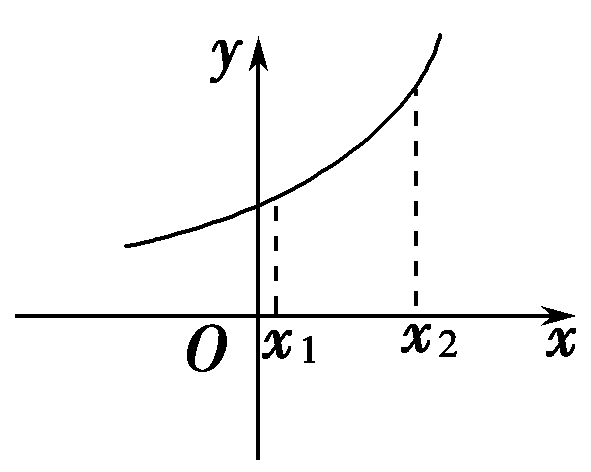
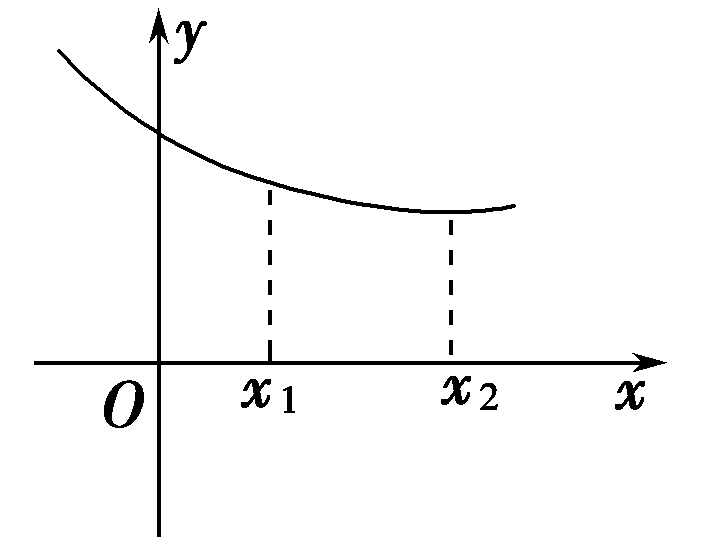
















 点击关注
点击关注











