数量 | 教你一分钟搞定“两次相遇”问题

★更多重庆选调备考资料请关注“金标尺公考“微信公众号

      重庆选调考试备考交流群：641199490   |       备考题库：金标尺公考APP

“多次相遇”问题是数量关系中的重难点，不仅考察方式多样，而且还需要搭配画图，这让很多同学望而却步。实际上这类题型中有一类叫做“两次相遇”问题，可以直接套公式搞定。

题型判定

单岸型：甲乙分别从相距S的A、B两地相向而行，第一次相遇距A地S1，第二次相遇距A地S2。

两岸型：甲乙分别从相距S的A、B两地相向而行，第一次相遇距A地S1，第二次相遇距B地S2。

题干往往会告诉我们S1、S2、S中两个量的值，求解第三个量。

解题公式

单岸型两次相遇：S=(3S1+S2)/2

双岸型两次相遇：S=3S1-S2

典型例题

【例1】甲乙两车同时从A、B两地相向而行，在距B地54千米处相遇，它们各自到达对方车站后立即返回，在距A地42千米处相遇。请问A、B两地相距多少千米(   )。

A.120   B.100   C.90   D.80

【金标尺解析】A。 方法一：根据题意先画图，设A、B两地相距S千米，第一次相遇在C点，BC距离为54千米，即乙车第一次相遇走了54千米；第二次相遇在D点，AD距离为42千米，乙车第二次相遇时走了AB+AD=S+42。根据两者异地多次相遇结论，乙车第二次相遇时所走的距离为第一次的3倍，即S+42=3×54，解得S=120，即A、B两地相距120千米。故本题答案为A项。

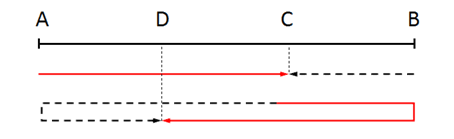
方法二：判断题型为两岸型两次相遇问题，直接代入公式S=3S1-S2=3×54-42=120千米。故本题答案为A项。

【点拨】比较两种方法，公式法的优势在于：①节省思考和分析问题的时间；②不用画图，解题过程简洁高效。

【例2】甲车从A地，乙车从B地同时出发匀速相向行驶，第一次相遇距离A地100千米。两车继续前进到达对方起点后立即以原速度返回，在距离A地80千米的位置第二次相遇。则AB两地相距多少千米（  ）。

A.170   B.180   C.190   D.200

【金标尺解析】C 判断题型为单岸型两次相遇问题。直接代入公式S=(3S1+S2)/2=(3×100+80)/2=190千米。故本题答案为C项。

【例3】甲、乙两汽车分别从P、Q两地同时出发相向而行，途中各自速度保持不变，他们第一次相遇在距P点16千米处，然后各自前行，分别到达Q、P两点后立即折返。第二次相遇是在距P点32千米处，则甲、乙两车的速度之比为（   ）。

A.2:3   B.2:5   C.4:3   D.4:5

【金标尺解析】A 判断题型为单岸型两次相遇问题。直接代入公式S=(3S1+S2)/2= (3×16+32)/2=40千米，第一次相遇甲走了16千米，则乙走了40-16=24千米，根据时间不变，路程与速度成正比，可知甲、乙两车的速度之比为16:24=2:3。故本题答案为A项。