当两个分数作比较时,若其中一个分数的分子与分母都比另外一个分数的分子与分母分别大一点,此时使用“差分法”可以很好地解决这样的问题。
我们定义分子与分母都比较大的分数叫“大分数”,分子与分母都比较小的分数叫“小分数”,而这两个分数的分子、分母分别做差得到的新的分数我们定义为“差分数”。
例如 (小分数),
(小分数), (大分数),我们将两个分数的分子、分母分别做差得(差分数),然后再用分数和小分数比较大小:
(大分数),我们将两个分数的分子、分母分别做差得(差分数),然后再用分数和小分数比较大小:
若差分数>小分数,则大分数>小分数;
若差分数<小分数,则大分数<小分数;
若差分数=小分数,则大分数=小分数。
对上述例子,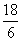 (差分数)>
(差分数)>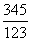 (小分数),则
(小分数),则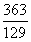 (大分数)>
(大分数)>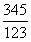 (小分数)。“差分法”本身是一种“精算法”而非“估算法”,得出来的大小关系是精确的关系而非粗略的关系,即是可推导证明的。
(小分数)。“差分法”本身是一种“精算法”而非“估算法”,得出来的大小关系是精确的关系而非粗略的关系,即是可推导证明的。

同理可证其他两种情况。
理论实战
【例1】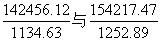
【解析】采用差分法进行比较,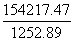 为大分数,
为大分数,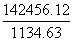 为小分数,构造差分数
为小分数,构造差分数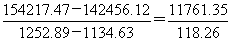 ,直除首位为1-,则
,直除首位为1-,则 (差分数)<
(差分数)<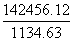 (小分数),则大分数
(小分数),则大分数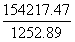 <
<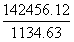 小分数。
小分数。
【例2】
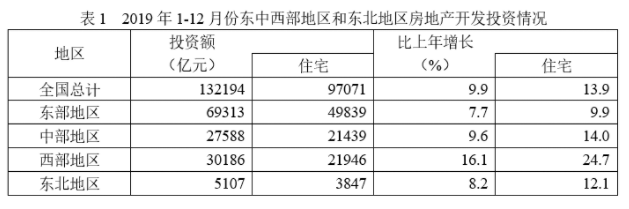
2.2019年全国住宅投资占房地产开发投资比重排名第一的地区是( )。
A.东部地区
B.中部地区
C.西部地区
D.东北地区
2.B 【解析】比重比较。由表1可知:东部占比为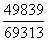 、中部
、中部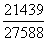 、西部
、西部 、东北
、东北 。优先选择分子分母较近的比较,
。优先选择分子分母较近的比较,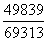 与
与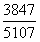 构造差分数为
构造差分数为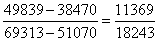 ,直除首位为7-,则东部
,直除首位为7-,则东部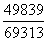 >东北
>东北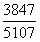 ,
,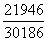 与
与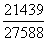 构造差分数为
构造差分数为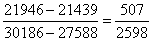 ,直除首位为2-,差分数<小分数,则西部
,直除首位为2-,差分数<小分数,则西部 <中部
<中部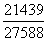 ,
,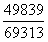 与
与 比较,构造差分数为
比较,构造差分数为 ,直除首位为7-,差分数<小分数,则东部
,直除首位为7-,差分数<小分数,则东部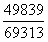 <中部
<中部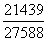 ,排名第一的为中部地区。故本题答案为B选项。
,排名第一的为中部地区。故本题答案为B选项。
【例3】(2012广东)
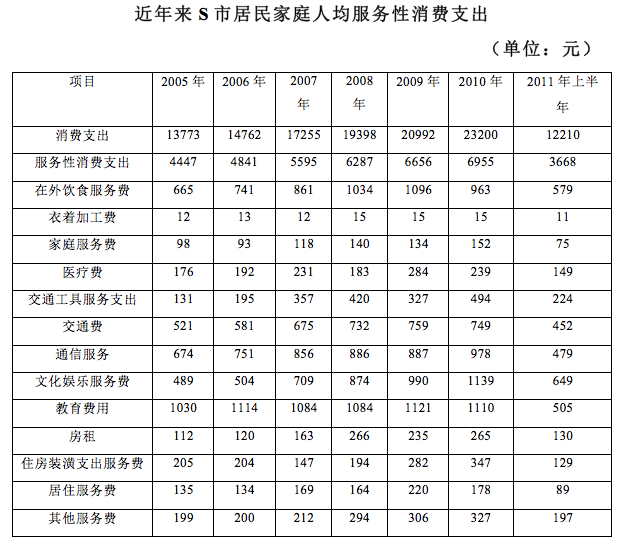
3.服务性消费支出占消费支出的比重最高的年份是( )年。
A.2005
B.2006
C.2007
D.2008
3.B【解析】比重比较。由图可知:2005年服务性消费支出占消费支出的比重为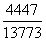 ,2006年为
,2006年为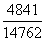 ,2007年为
,2007年为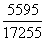 ,2008年为
,2008年为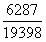 。采用差分法比较,优先选择分子分母较近的比较,
。采用差分法比较,优先选择分子分母较近的比较,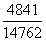 与
与 构造差分数为
构造差分数为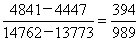 ,直除首位接近4,差分数>小分数,则大分数
,直除首位接近4,差分数>小分数,则大分数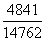 >小分数
>小分数 ,
,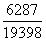 与
与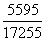 构造差分数为
构造差分数为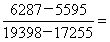
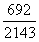 直除前两位为32,不好比较,此时不必着急,再做一次差分法,
直除前两位为32,不好比较,此时不必着急,再做一次差分法,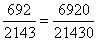 与小分数
与小分数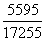 比较,构造二级差分数
比较,构造二级差分数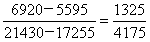 ,直除前两位31,则二级差分数>小分数,差分数
,直除前两位31,则二级差分数>小分数,差分数 >小分数,可得大分数
>小分数,可得大分数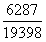 >
>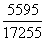 ,
,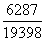 与
与 构造差分数为
构造差分数为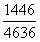 ,直除前两位为0.31,差分数<小分数,则大分数
,直除前两位为0.31,差分数<小分数,则大分数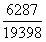 <小分数
<小分数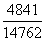 (2006年)。故本题答案为B选项。
(2006年)。故本题答案为B选项。
如果两个分数相隔非常近,我们甚至需要运用两次差分法,这种情况相对比较复杂,但如果运用熟练,同样可以大幅度简化计算。采用差分法进行比较,能够极大的提高我们比较的速度,差分法是绝技,需要技穷时再使用,这样才能做到又快又准的完成比较类题目。
 地区
地区 考试科目
考试科目 微信
微信

 微博
微博 抖音
抖音 023-67417095
023-67417095























 点击关注
点击关注











