
【导读】【每日一练】一阶非齐次线性微分方程。重庆教师招聘考试复习资料2021.11.10。更多教师招考信息,备考干货,辅导课程,时政资料,欢迎关注重庆教师招聘网。
一阶非齐次线性微分方程
1.微分方程的解
1.微分方程的解:若将函数代入微分方程,使该方程成为恒等式,这个函数称为微分方程的解。设y=y(x) 在区间I上连续且有直到n阶的导数,使 ,则称为该微分方程在区间I上的一个解。
,则称为该微分方程在区间I上的一个解。
2.微分方程的通解:若方程的解中含有独立的任意常数,且任意常数的个数与方程的阶数相同,则这样的解称为方程的通解。
3.初始条件与特解:确定通解中任意常数的条件: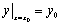 ,
, 称为初始条件。
称为初始条件。
2.一阶非齐次线性微分方程
1.定义:形如 的一阶方程称为一阶非齐次线性方程。
的一阶方程称为一阶非齐次线性方程。
2.通解公式: 。
。
3.推导计算公式:在方程两边同时乘以![]() 得
得
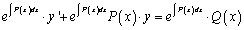 。
。
两边积分,得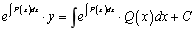 ,则
,则 。
。
【注】在一阶线性微分方程的通解公式 中,若
中,若 ,
,
则 ,
, ,代入上述公式中,有
,代入上述公式中,有
 ,
,
令 ,则有
,则有 。
。
其中,D依然为任意常数,故![]() 可不加绝对值。
可不加绝对值。
【例】求微分方程 满足初始条件
满足初始条件 的特解。
的特解。
【金标尺解析】本题主要考察微分方程——一阶非齐次线性微分方程。
因为 ,满足一阶线性微分方程,可得
,满足一阶线性微分方程,可得
 ,
,
因为 ,所以有
,所以有 。
。
所以 。
。
10.16教师联考《数学学科知识》通关班
教师面试《数学》说课+试讲
 地区
地区 考试科目
考试科目 微信
微信

 微博
微博 抖音
抖音 023-67417095
023-67417095


















 点击关注
点击关注











