【导读】二重积分的计算——平面直角坐标系!更多教师招考信息,备考干货,辅导课程,时政资料,欢迎关注金标尺教育。
知识点:二重积分的计算——平面直角坐标系
在直角坐标系中,常用平行于x轴y轴的两组直线来分割积分区域D,则除了包含边界点的一些小闭区域外,其余的小闭区域都是矩形闭区域。设矩形闭区域![]() 的边长为
的边长为![]() 和
和![]() ,于是
,于是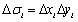 。故在直角坐标系中,面积微元
。故在直角坐标系中,面积微元![]() 可记为dxdy,即
可记为dxdy,即 。进而把二重积分记为
。进而把二重积分记为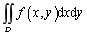 ,这里我们把dxdy称为直角坐标系下的面积微元。
,这里我们把dxdy称为直角坐标系下的面积微元。
本节介绍的二重积分的计算方法,其基本思想是将二重积分化为两次定积分来计算,转化后的这种两次定积分常称为二次积分或累次积分。
1. X型积分区域
若积分区域D可以用不等式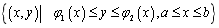 来表示,其中函数
来表示,其中函数![]() 、
、![]() 在区间[a,b]上连续,这样的区域称为X型区域,其区域特征为:穿过D内部且平行于y轴的直线与D的边界最多相交与两点,大致的函数图形是由上下两个函数夹击而成的样子(如图)。
在区间[a,b]上连续,这样的区域称为X型区域,其区域特征为:穿过D内部且平行于y轴的直线与D的边界最多相交与两点,大致的函数图形是由上下两个函数夹击而成的样子(如图)。
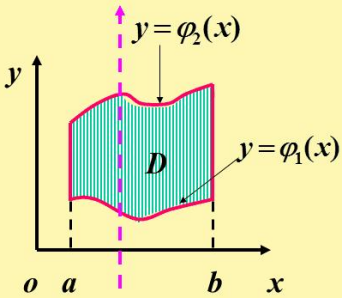
一般地,若D是由x=a,x=b, ,
,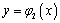 所围成的X型闭区域,求以D为底,以曲面z=f(x,y)(f(x,y)连续且非负)为顶的曲顶柱体的体积,垂直于x轴,可以过x轴上的任一点x做曲顶柱体的截面,则截面面积是以
所围成的X型闭区域,求以D为底,以曲面z=f(x,y)(f(x,y)连续且非负)为顶的曲顶柱体的体积,垂直于x轴,可以过x轴上的任一点x做曲顶柱体的截面,则截面面积是以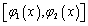 为底,以z=f(x,y)为顶的曲边梯形,其面积为
为底,以z=f(x,y)为顶的曲边梯形,其面积为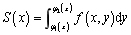 。
。
对应的立体体积为
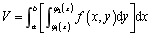 。该积分是先y后x次序的二次积分,也可以记作
。该积分是先y后x次序的二次积分,也可以记作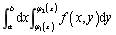 。
。
2. Y型积分区域
若积分区域D可以用不等式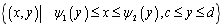 来表示,其中函数
来表示,其中函数![]() 、
、![]() 在区间[c,d]上连续,这样的区域称为Y型区域,其区域特征为:穿过D内部且平行于x轴的直线与D的边界最多相交与两点,大致的函数图像是由左右两个函数合抱而成的样子(如图)。
在区间[c,d]上连续,这样的区域称为Y型区域,其区域特征为:穿过D内部且平行于x轴的直线与D的边界最多相交与两点,大致的函数图像是由左右两个函数合抱而成的样子(如图)。

若D是由y=c,y=d,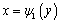 ,
,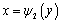 所围成的Y型闭区域,求以D为底,以曲面z=f(x,y)为顶的曲顶柱体的体积,垂直于y轴,可以过y轴上的任一点y做曲顶柱体的截面,则截面面积是以
所围成的Y型闭区域,求以D为底,以曲面z=f(x,y)为顶的曲顶柱体的体积,垂直于y轴,可以过y轴上的任一点y做曲顶柱体的截面,则截面面积是以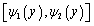 为底,以z=f(x,y)为顶的曲边梯形,其面积为
为底,以z=f(x,y)为顶的曲边梯形,其面积为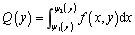 。
。
对应的立体体积为
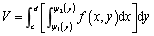 。该积分是先x后y次序的二次积分,也可以记作
。该积分是先x后y次序的二次积分,也可以记作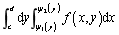 。
。
典型例题
【例】计算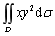 ,其中D是由直线y=1,x=2及y=x所围成的闭区域。
,其中D是由直线y=1,x=2及y=x所围成的闭区域。
【金标尺解析】本题考查多元函数微积分学——二重积分。
【金标尺答案】![]()
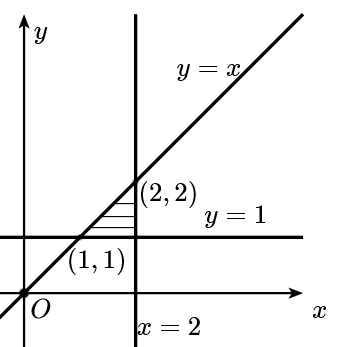
把区域写成X型表达式,
则有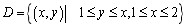 ,所以
,所以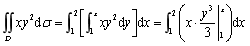
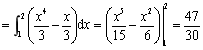 。
。
把区域写成Y型表达式,
则有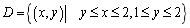 ,所以
,所以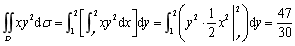 。
。
 地区
地区 考试科目
考试科目 微信
微信

 微博
微博 抖音
抖音 023-67417095
023-67417095





















 点击关注
点击关注











