重庆事业单位《职测》数量关系：勾股定理

近年来，职测数量关系越来越重视几何板块的考查，这类题往往具有一定难度，常常是考试中拉开分差的关键。今天金标尺就和大家分享几何问题中常考题型之一--勾股定理，相信各位考生在学习后，都能快速识别并解决这类问题。接下来大家一起来跟金标尺学习吧!

一、勾股定理的定义

勾股定理，是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理，也有人称“商高定理”。

定义在平面上的一个直角三角形中，两个直角边边长的平方加起来等于斜边长的平方。如果设直角三角形的两条直角边长度分别是a和b，斜边长度是c，那么可以用数学语言表达：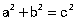

二、常见勾股数

常考勾股数组：（3、4、5）；（6、8、10）；（5、12、13）

对于常考的勾股数组，可以在备考时熟练记忆，做题时直接运用，可节省思考和推算时间。

包含特殊角的直角三角形三边比例关系：

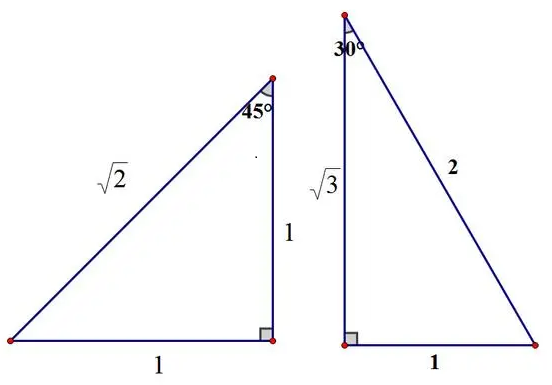
45°、45°、90°三角形三边比例：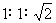

30°、60°、90°三角形三边比例：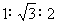

熟练记忆30°角和45°角的直角三角形三边比例关系，已知其中一条边的长度便可推出其余两条边的长度，这一性质在直角三角形的考题中经常考到。

下面让我们通过这几道题练习一下吧！

【例1】两名学生从同一点往相反方向出发，各行8米后左转，再各行6米，此时两人之间最短距离是（  ）米。

A.0

B.10

C.20

D.30

【金标尺解析】如图所示，两人从M出发，分别走到A、B两地后左转到达C、D，则两人之间的最短距离为CD的长。根据勾股定理可得，CM=DM=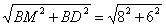=10米，则CD=CM+MD=20米。故本题答案为C项。

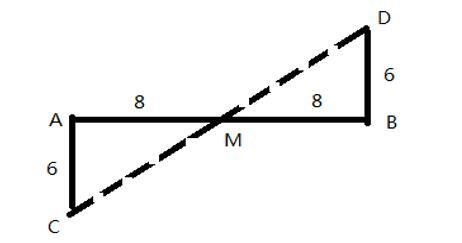
【例2】升旗仪式上，小明注意到从他仰角30°正好能望向升旗台底部，仰角60°正好能望向旗杆顶端。已知小明身高1.5m，旗杆高6m，则升旗台距地面（  ）m。

A.6

B.4.5

C.3

D.1.5

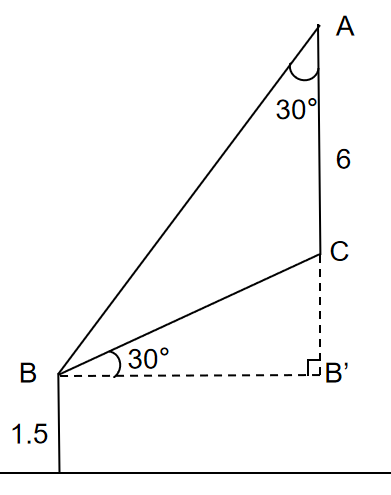
【金标尺解析】如图所示，设小明的头顶为点B，升旗台底部为点C，旗杆顶端为点A，根据题意，可得∠CBB’=30°，∠ABB’=60°，则∠ABC=∠BAC=30°，△ABC为等腰三角形，故BC=AC=6m，在直角三角形CBB’中，根据勾股定理可求得CB’=3m，则升旗台距地面3+1.5=4.5m。故本题答案为B项。

总结：相信学到这儿时，大家都清楚地掌握了勾股定理的做题方法。同学们记得平时要多多练习，才能融会贯通~