判推 | 如何将《三体》的降维打击运用到几何问题上？

科幻电影《流浪地球》的爆红，让刘慈欣的更多作品为大家所熟知。大刘的《三体》中有一种致命的武器叫做“二向箔”，能够对太阳系进行三维到二维的降维打击，非常震撼！今天我们就来学习降维打击在几何问题中的应用——降维打击法求解立体图形“最短路径问题”。

题型判定：

求解立体图形中两点之间的最短路程/距离。

解题步骤

1.将立体图形展成平面图形；

2.求平面展开图上两点间最短距离；

下面通过例题进一步了解立体图形最短路径问题的解题思路。

典型例题

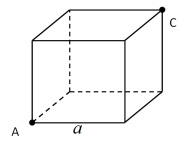
【例1】一只蚂蚁从下图的正方体的顶点沿正方体的表面爬到正方体的顶点，设正方体边长为，问该蚂蚁爬过的最短路程为（    ）

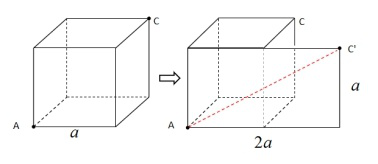
【例2】如图，正四面体ABCD，P、Q分别是棱AB、CD的三等分点和四等分点（AB=3AP=4CQ），棱AC上有一点M，要使M到P、Q距离之和最小，则MC∶MA=（     ）。

1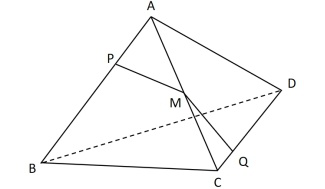

A.1∶2

B.4∶5

C.3∶4

D.5∶6

【金标尺解析】C。判断本题为立体图形最短路径问题。如下图所示，将正四面体右侧面展开得到平行四边形ABCD，连接PQ交AC于M点，得到M到P、Q距离之和最小值PQ。赋值棱长为12，则AP=4，CQ=3。再由△APM与△CQM相似，对应边成比例，可知MC:MA=CQ:AP=3:4。故本题答案为C项。

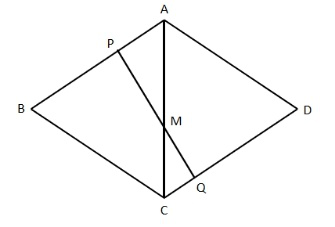
通常来说，数量关系中几何问题考察方式多样、整体难度较高。但是立体图形中的最短路径问题套路性非常强，只需稍加培养空间想象力，采用降维打击，将三维立体图形转换为二维平面图形，即可快速求解正确答案。

   更多资讯，扫描下方二维码